Derivation of Franka’s Inertia Parameters

The original values are derived from Figure 4 of the paper from Ledezma, Fernando Diaz and Haddadin, Sami. For the \(i\)-th link, the mass \(m\), mass times the center of mass location \(mc_x\), \(mc_y\), \(mc_z\), and the 6 paramters of the inertia tensor matrix, \(I_{xx}\), \(I_{xy}\), \(I_{xz}\), \(I_{yy}\), \(I_{yz}\), \(I_{zz}\) about the center of mass are:

Linkage	\(m\) (\(kg\))	\(mc_x\), \(mc_y\), \(mc_z\) (\(kg\cdot m\))	\(I_{xx}\), \(I_{xy}\), \(I_{xz}\), \(I_{yy}\), \(I_{yz}\), \(I_{zz}\) (\(kg\cdot m^2\))
Link 1, \(i=1\)	4.9707	(0.0193, 0.0103, -0.4654)	(0.7470, -0.0002, 0.0086, 0.7503, 0.0201, 0.0092)
Link 2, \(i=2\)	0.6469	(-0.0020, -0.0186, 0.0023)	(0.0085, -0.0040, 0.0103, 0.0281, 0.0008, 0.0265)
Link 3, \(i=3\)	3.2286	(0.0888, 0.1267, -0.2147)	(0.0565, -0.0082, -0.0055, 0.0529, -0.0044, 0.0182)
Link 4, \(i=4\)	3.5879	(-0.1908, 0.3746, 0.0985)	(0.0677, 0.0277, 0.0039, 0.0324, -0.0016, 0.0776)
Link 5, \(i=5\)	1.2259	(-0.0147, 0.0503, -0.0471)	(0.0394, -0.0015, -0.0046, 0.0315, 0.0022, 0.0109)
Link 6, \(i=6\)	1.6666	(0.1002, -0.0235, -0.0175)	(0.0025, 0.0015, -0.0001, 0.0106, 0.0001, 0.0118)
Link 7, \(i=7\)	1.4655	(0.0004, -0.0031, 0.1453)	(0.0308, 0.0004, -0.0007, 0.0284, -0.0005, 0.0067)

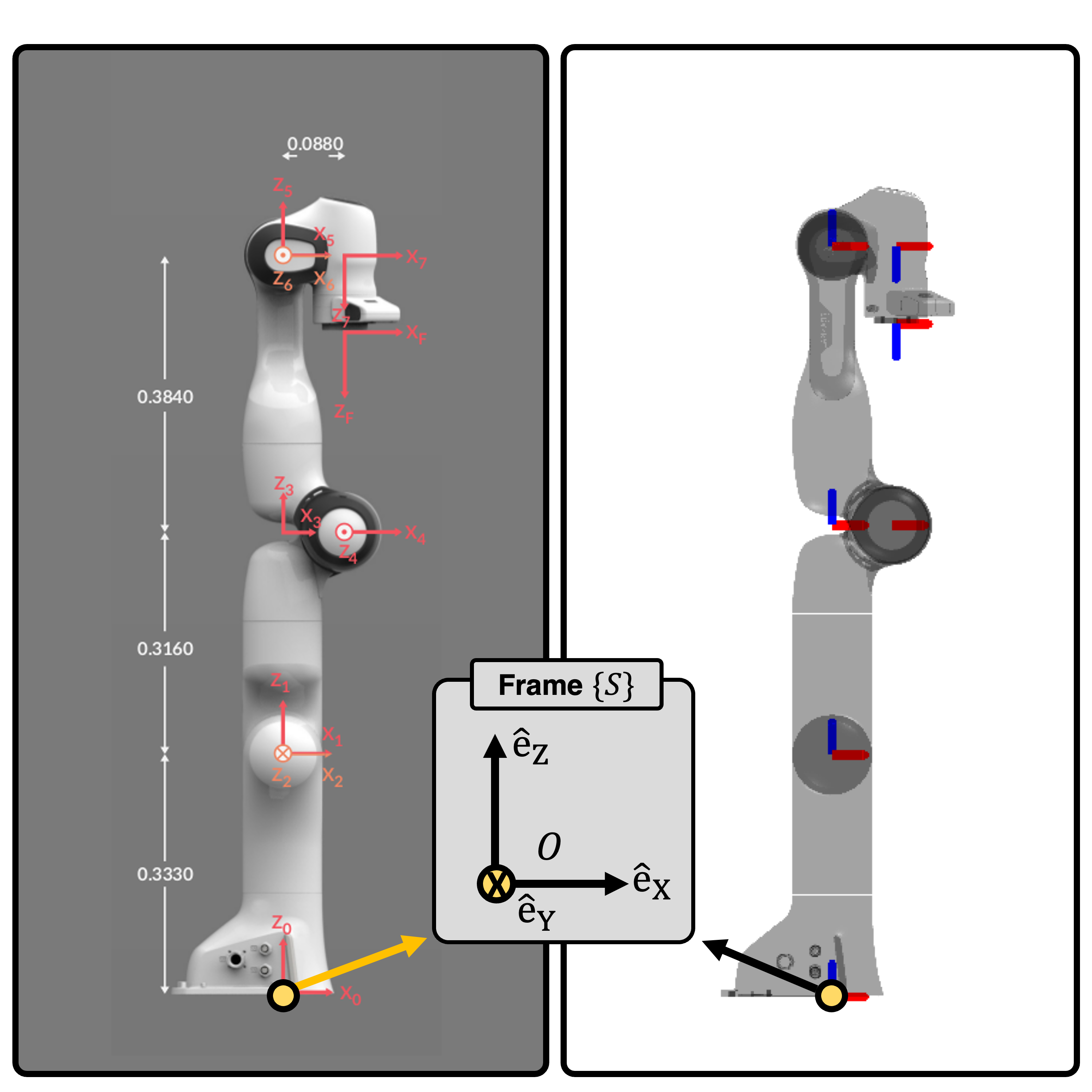
The inertial parameters of the \(i\)-th link are described with respect to the frame on the \(i\)-th joint. This frame is defined by the Denavit–Hartenberg (DH) parameters. The DH parameters for the Franka can be found on this website and are shown below:

Joint	\(a\) (m)	\(d\) (m)	\(\alpha\) (rad)	\(\theta\) (rad)
Joint 1	0	0.333	0	\(\theta_1\)
Joint 2	0	0	\(-\pi/2\)	\(\theta_2\)
Joint 3	0	0.316	\(\pi/2\)	\(\theta_3\)
Joint 4	0.0825	0	\(\pi/2\)	\(\theta_4\)
Joint 5	-0.0825	0.384	\(-\pi/2\)	\(\theta_5\)
Joint 6	0	0	\(\pi/2\)	\(\theta_6\)
Joint 7	0.088	0	\(\pi/2\)	\(\theta_7\)

Let the frame attached at the i-th joint be denoted as \(\{i\}\). For \(i=1,2,\cdots, 7\), the relation between frame \(\{i\}\) and \(\{i-1\}\) is:

\[\begin{split}{}^{i-1}H_{i} = \begin{bmatrix} \cos \theta_i & -\sin\theta_i & 0 & a_i \\ \sin \theta_i \cos \alpha_i & \cos\theta_i \cos \alpha_i & -\sin\alpha_i & -d_i\sin\alpha_i \\ \sin \theta_i \sin \alpha_i & \cos\theta_i \sin \alpha_i & \cos\alpha_i & d_i\cos\alpha_i \\ 0 & 0 & 0 & 1 \end{bmatrix}\end{split}\]

Subscript \(i\) denotes the DH parameter of joint \(i\). Moreover, frame \(\{0\}\) is equal to the fixed frame \(\{S\}\) attached at the origin.

From this, we can find the frame attached at the \(i\)-th joint by matrix concatenation:

\[\begin{split}\begin{align} {}^{S}H_{1} &= {}^{S}H_{1} \\ {}^{S}H_{2} &= {}^{S}H_{1} {}^{1}H_{2} \\ {}^{S}H_{3} &= {}^{S}H_{1} {}^{1}H_{2}{}^{2}H_{3} \\ & ~~~~~~~ \vdots \\ {}^{S}H_{7} &= {}^{S}H_{1} {}^{1}H_{2}{}^{2}H_{3} {}^{3}H_{4}{}^{4}H_{5}{}^{5}H_{6}{}^{6}H_{7} \\ \end{align}\end{split}\]

The result plotted in Exp[licit] (right) is consistent with the result shown from the franka website (left).

Let the CoM location of the \(i\)-th link, expressed in frame \(\{i\}\), be denoted as \({}^{i}\mathbf{c}_i := [{}^{i}c_{x,i},{}^{i}c_{y,i},{}^{i}c_{z,i}]\), (shown in the table above). We need to map these values from frame \(\{i\}\) to frame \(\{S\}\). Thus, for \(i=1,2,\cdots,7\):

\[\begin{split}\begin{bmatrix} {}^{S}\mathbf{c}_i \\ 1 \end{bmatrix} = {}^{S}H_i \begin{bmatrix} {}^{i}\mathbf{c}_i \\ 1 \end{bmatrix}\end{split}\]

From this, we find the position of the CoM, expressed in frame \(\{S\}\). The detailed location and its values are posted in this section.

Finally, we derive the moment of inertia, but with respect to the axes of frame \(\{S\}\). Let the moment of inertia about frame \(\{i\}\) be represented by matrix \({}^{i}\mathbf{I}_i\). To express with respect to frame \(\{S\}\) we use the following mapping:

\[{}^{S}\mathbf{I}_i = {}^{S}\mathbf{R}_i ~ {}^{i}\mathbf{I}_i ~ {}^{S}\mathbf{R}_i^{\text{T}}\]

In this equation \({}^{S}\mathbf{R}_i\in SO(3)\), which can be derived from \({}^{S}\mathbf{H}_i\). This eventually gives us the inertia matrix shown in this section.